The Emerald Polyhedra

Basic Elements

The Ancient Greeks were engaged in a never-ending quest to more accurately define the world around them. Doing this allowed them to deal with reality as it factually is, carrying on their affairs with great success, leading to a flourish in art and music, causing justice to reign throughout their lands and assuring a purpose for their people.

Of all the systems of measurement humankind has created, mathematics is one of the most precise. Even simple arithmetic statements such as, "There are three apples on the table", allow for exact numerical understandings. To define the physical surface and volume of those apples requires the branch of mathematics known as Geometry -- the study of forms and shapes.

The word Polygon comes from Greek, meaning Many Angles. Most basic shapes children learn to identify are Regular Polygons -- figures composed only of equal angles (equiangular) and equal sides (equilateral). A few well-known examples are the Triangle (3 sides), the Square (4 sides), the Pentagon (5 sides) and the Hexagon (6 sides). Other polygons include shapes which are equiangular like the Rectangle or equilateral like the Diamond.

Basic Polygons

Polyhedra means Many Sides. A Polyhedron is created by extending all points of a two-dimensional Polygon into lines of equal length, resulting in a three-dimensional shape. When looking onto the top of a Red Emerald crystal, the geometric shape of a six-sided Hexagon is typically observed. When a two-dimensional hexagon is stretched into three-dimensions (Hexagonal Stellation), a six-sided tower is formed.

To imagine this process, think of a two-dimensional hexagon whose points are in a single geometric plane. On a parallel plane hovering in front of the first, create a second hexagon mirroring the original. Draw lines between their corresponding points to form a three-dimensional figure. This "pushing forward" or "bursting forth" into the third dimension is known as Stellation.

Stellation of 2D Hexagonal Polygon into a 3D Prismatic Polyhedron

In geometry, the process of extending a two-dimensional polygon into a three-dimensional polyhedron begins with an original figure, extending edges into facial planes, usually in a symmetrical way, until they form the closed boundary of a new figure. The new figure is a Stellation of the original. The word comes from the Latin stellātus , "starred ", which in turn comes from Latin stella , "star ".

~ Wikipedia Entry: Stellation

In the Cosmos, stars form when clouds of matter fuse together in dense combinations. In the Earth, gemstones form when supersaturated matter fuses together in dense mineral crystallizations. These two natural phenomena share mesmerizing parallels parallels as both stars and gemstones are products of high-energy situations dispensing concentrated power.

Atom translates as Uncuttable, meaning unable to be divided. This definition implies an atomic unit is the smallest possible unit (or smallest usable unit) in any system of measurement. The Periodic Table is a complete list of the Elements, or the known set of atomic units which make up all matter in our universe.

In an Emerald molecule, a beryllium atom locks six oxygen atoms in a six-sided ring. Molecules are shaped equally, so the number of arrangements in which their geometric forms can fit together is finite. These identical figures are organized in exactly the same highly-ordered manner over and over and over again in every gem crystal.

A Crystal is an element or mineral whose molecules are so highly-ordered that regular polygons can be observed in its physical form. Plato identified the simplest physical shapes, known as the Platonic Solids, but the full set of Uniform Polyhedra (enclosed three-dimensional polygonal geometries) in which a mineral habit may form was not completely described until 1900.

Six light triangles over six dark triangles represent molecular stacking

in a beryl unit cell

Single molecules cohere with one another using chemical bonds to form larger groups. The smallest number of molecules required to band together, or the atomic unit of a crystal, is called the Unit Cell. In 1848, a French physicist named Auguste Bravais discovered that just as there are a finite number of basic polygons, the smallest molecular unit can also assume only a limited number of geometric shapes.

A magnified jardin unveils parallel horizontal fingerprint inclusion lines, (bottom right, top) revealing the invisible grid on which our universe is built

Because crystals utilize a repeating pattern to stack molecular groups which are always the same size, the spacing between unit cells is meta-consistent. Bravais developed a system using parallel lines along unit cell boundaries as markers to imagine a grid or Lattice. Differences in lattice spacing allowed classification of minerals into Crystal Systems.

To investigate the Hexagonal Crystal System, let's return to the two-dimensional Hexagon with all points in a single geometric plane. Imagine a second parallel plane and create a hexagon mirroring the first. Now think of these shapes as beryl molecules. Drawing lines between their corresponding points is their attempt at making a chemical bond.

Beryl molecules use chemical bonds to form a Wafer

Connecting hexagon-face-to-hexagon-face allows for the most surface contact and cohesion, but the more connections with other unit cells a newly-attached group can establish, the stronger their bond to the larger crystal will be. A reinforced union increases the probability of incorporation due to burial. To be permanently integrated after initial attachment, a molecule must be "buried" or surrounded by unit cells on all sides.

Crystallization occurs in a temperature range continuously fluctuating above and below the saturation threshold of the mineralizing solution (or mineral-rich volcanic vapor), potentially causing weakly-coupled molecules to be re-dissolved. Net attachment or detachment of molecules to a crystal surface determines the rate of growth or dissolution, respectively.

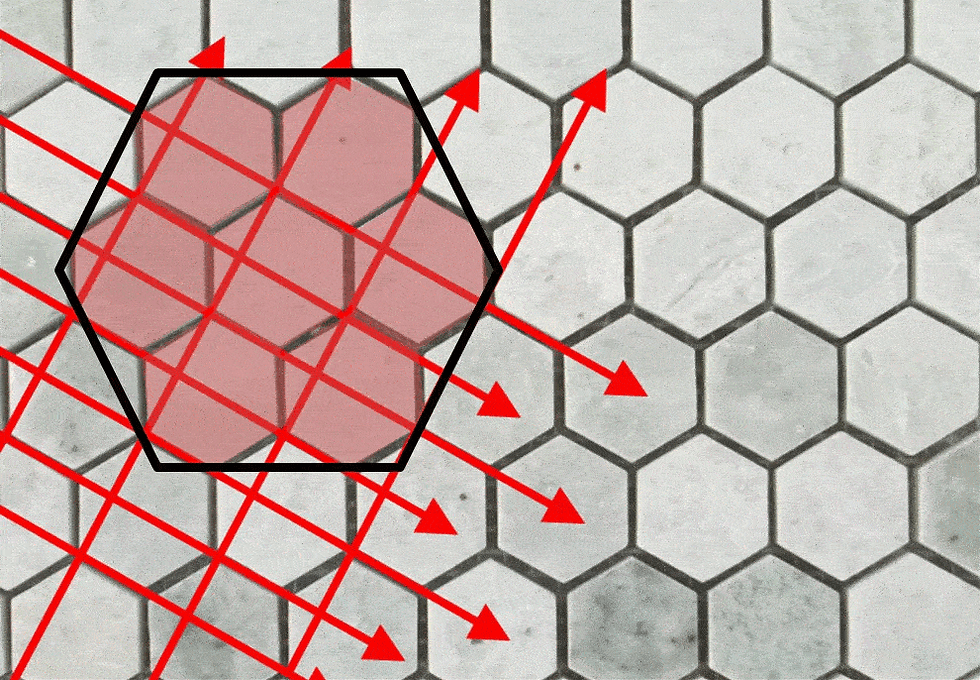
Red lattice lines show the grid unit cells use as a foundation to construct a wafer, then a prismatic plateau, incorporating molecules by burial

Once a hexagon has affixed to a surface, other unit cells preferentially attach where they can make two connections -- to the surface AND to the side of another group. During crystallization, thousands of these hexagonal groups grow across a surface simultaneously, at different rates, sizes and elevations.

Stacking hexagons row by row and depositing one layer on top of another allows a crystal to form glassy faces without a single group or island significantly outpacing another. As independent islands coalesce, groups become more interlaced with the greater crystal structure, which becomes more stable.

Sustained waves of synthesis on the molecular level stack into layers

which become tiny wafers perceptible on the human level

In geometry, a Prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first [in mineral specimens, the bases of a prism are called Termination Ends], and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases.

~ Wikipedia Entry: Prism

Continued hexagonal stacking over a prolonged period will result in the formation of larger specimens. A Wafer (tabular) will become a Square Prism (equant) when the length of its sides equals the width. When the length becomes longer than the width of a crystal structure, the habit has become a Rectangular Prism (elongated).

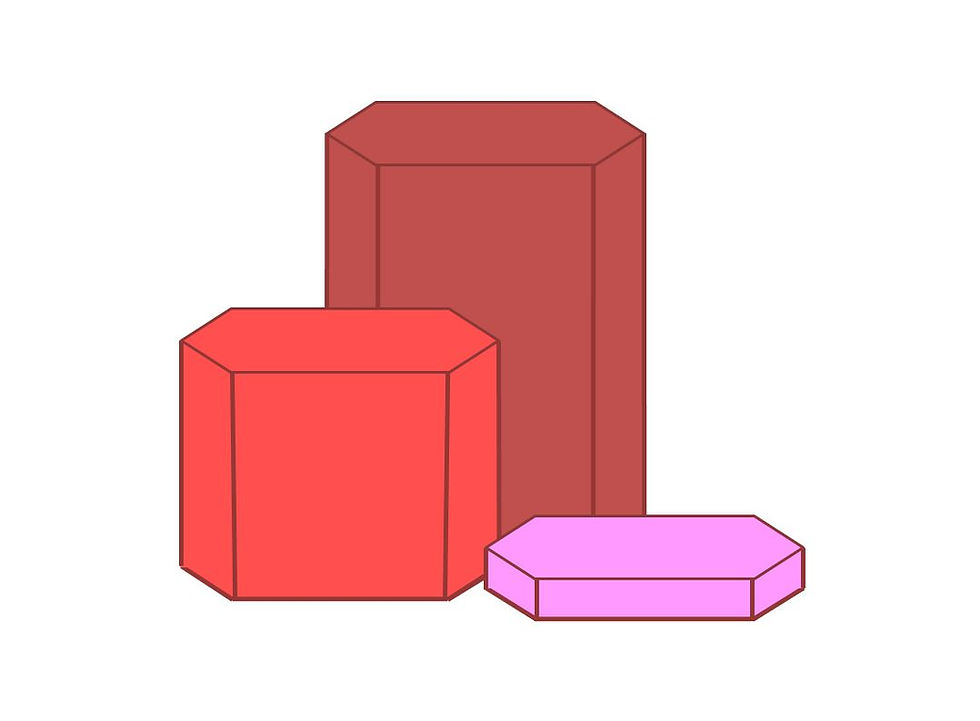
Stages of the Six-Sided Tower

Tabular Wafer (Right), Square Prism (Left) and Rectangular Prism (Back)

These crystals represent the purest forms of the mineral beryl. Beryl produces precious and semi-precious stones, because a tremendous amount of beryllium is required for crystallization, and beryllium is a rare element, with a very low incidence in the earth's crust.

In the coming months, we will continue to investigate modifications to the typical geometric structures that Red Emerald crystals display, along with methods to evaluate and describe these features yourself!